The settling time [1] of a dynamical system [2] is the time from the application of an ideal instantaneous step input to the time at which the system output has entered and remained within a specified tolerance (also known as the error band).
This tool calculates the settling time for a second order system with a damping ratio ζ less than 1.
Enter:
- Tolerance T% (this is the level to which a signal is considered as settled)
- Damping Ratio ζ
- Natural frequency fn (Hz)
Formula
TS = -Loge(0.01*T%* √(1-ζ2))/( ζ*2*π*fn)
Example Calculation
For a tolerance of 2%, damping ratio of 0.5 and natural frequency 100 Hz, the settling time is 13 ms. As the tolerance decreases to 1%, the settling time increases to 15 ms.
Background
What is settling time?
Settling time refers to the time it takes for a system to reach a steady-state condition after a change in input or disturbance. It represents the period required for the system’s output to settle within a specified limit or tolerance (typically 5% or lower).
In engineering and control systems, settling time is an important parameter that determines the system’s ability to respond accurately and quickly to changes.
The settling time is generally measured from the instant the system undergoes a perturbation, such as a step change in input, to the point where the output remains within a specified percentage of the final value. This is shown in the picture below.
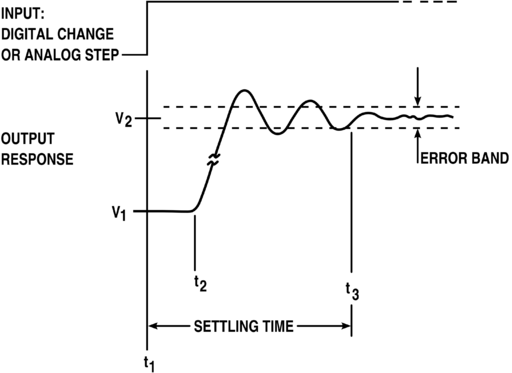
A shorter settling time indicates a faster response while a longer settling time results in delayed outputs.
In general, a step response should be characterized by
- fast rise time
- quick settling
- with low overshoot
What is a second-order system?
In a second order system, the dynamics and responses are described by second order differential equations. These systems can be found in a variety of engineering applications. The unit step response of such systems can be analyzed to understand their behavior. The overshoot, or the maximum deviation from the steady-state value for example, is an important parameter to assess the system’s performance.
The transfer function of a second order system is typically denoted as a ratio of polynomials, which allows us to analyze its behavior in the frequency domain. The response of a second order system can be classified as
- underdamped
- critically damped
- overdamped
based on its damping ratio. The underdamped response is characterized by oscillations in the transient response, while the critically and overdamped responses decay without oscillations.
The natural frequency of a second order system determines the rate of decay of its transient response. By visualizing the time domain response and analyzing its exponential behavior, we can gain insights into the system’s stability and performance.
A circuit that consists of a Resistor (R), Inductor (L) and Capacitor (C) – also known as an RLC circuit, is an example of a second order system.
Practical applications
In the case of data acquisition systems, the settling time of an operational amplifier (Opamp) is a critical parameter. To guarantee accuracy, the Opamp output must settle before the analog-to-digital converter (ADC) can accurately digitize the data.
It is recommended that the Opamp output settle to within 1 LSB of final value of the ADC that is being driven within a time period that is dictated by the sampling rate of the system.
Related Calculators
Wikipedia References
[1] Settling Time
[2] Dynamical System
[3] RLC Circuit
